$Icons 1423866245 discovery fractals$ Fractals

Activity 1
Activity 2
Activity 3
Activity 4
Activity 5
Review
Explore
Relate
Gallery

Description backgrounds 1718120452 drift

Snowflakes are design, crystals are design, music is design, and the electromagnetic spectrum which the rainbow of colors are but one millionth of its range is design. Buckminster Fuller

Take a look around you. Take in the clouds in the sky, the leaves on the trees, the waves in the ocean. These are all patterns in nature. Nature is constantly evolving and always changing. For everything that exists, there is a purpose, and that purpose connects to other purposes.

Watch BBC How Fractals Help Us Understand the Universe

Activity 1 – Fractals and the Universe

$Backgrounds 1717866351 fractal a1$

In the century of two grand theories- the Theory of Relativity and the Theory of Quantum Physics, a mathematician, Benoit Mandelbrot, became fascinated by natural patterns. He studied patterns like branching patterns in the leaves of trees, the tributaries of rivers, and the human circulatory system. He saw repeating patterns in the changing clouds, the motion of ocean waves, and dune ripples. He discovered that the visualization of vibrations and our heartbeats are all subsets of repetitive patterns. At first glance, the detailed patterns looked different and chaotic, but at closer observation, patterns of self-similarity, repetition, and changes in scale began to connect an order beneath the chaos. Mandelbrot coined these patterns in the Universe across all scales as fractals. Today, from quantum physics to astrophysics to metaphysics, humans are beginning to understand that there is order within the seeming chaos of the Universe.

Step outside. Look down. Look out. Look up. Photograph patterns in the world that you live in make a posture of fractal patterns. Upload it to the gallery!

Activity 2 – Fractals and Nature

$Backgrounds 1717796635 fractal scavange hunt$

Fractals can be seen everywhere you look in nature, in an infinite number of scales, whether it be the erosion in the landscape of a valley, or a stream, or a coast line, or the patterns in the branches, it is all connected. For this first activity look around for examples of fractals. You might find some examples in your very own kitchen like broccoli! Once you have found one, try and find a similar looking one, but at a completely different scale. Step outside and look down, look out, and look up. Believe it or not, you can find examples of fractals in what you stand on, in what is in the soil, what comes from the soil, what plant shape and tree branching contribute, what patterns rivers make in the landscape, what crystals, and bubbles share. Start looking around for patterns in nature that repeat themselves. Make sketches or take photographs.

Activity 3 – The Koch Snowflake

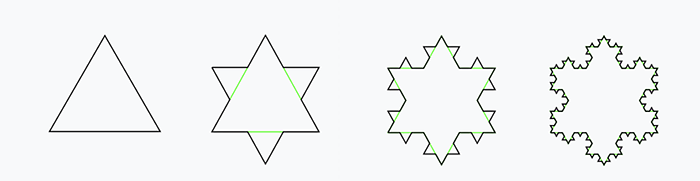
$Backgrounds 1719080368 fractals koch a3$

The generation of a Koch snowflake begins with a 3-sided equilateral triangle. In 1904, the Swede, Helge von Koch, generated a Koch curve that was infinite, but encapsulated a finite area. On each side of the triangle, he split the side into three parts. In the middle part of each of the three sides, he created three new equilateral triangles. (Image 2) He continued to iterate this process at a smaller scale (Image 3) and a fourth smaller scale (Image 4) and the Koch snowflake was born! Follow the four steps and replicate a Koch Snowflake. Be aware of fractals in nature, in science, in mathematics, connecting theory with philosophy and life in the world! Upload your Koch Snowflake to the gallery!

Activity 4 – The Sierpinski Triangle

$Backgrounds 1719082287 fractalstri a4$

The Sierpinski Triangle is another example of fractal building starting with an equilateral triangle. Instead of dividing the sides into thirds, divide the original triangle into four equal triangles and remove the central triangle. Now divide the top and two side triangles into four smaller equal triangles in each of the four black triangles continuing to remove the central triangle. Keep taking the remaining black triangles and dividing them into 4 smaller triangles and you will be self-replicating! Upload your triangles and check out the Fractal Foundation’s Sierpinski Triangles! Upload yours to the gallery!

Activity 5 – Fractals: Order in the Chaos

$Backgrounds 1719082481 fractals a4$

“Nature uses only the longest threads to weave her patterns so that each small piece of her fabric reveals the organization of the entire tapestry. Richard P. Feynman

“I believe a leaf of grass is no less than the journey work of the stars.”* Walt Whitman, poet

We have been given the gift of the Earth to call home. It is important to be aware that the Earth’s health is our health, and our health is connected to the Earth’s health. Our life on this planet is tied to nature’s 3.5 billion years of evolution as well as to our contributions since we arrived. Explore PBS The Age of Nature to discover how our life is dependent on the nature around us. The Earth is made for all kinds of forms of life that are critical to our food chain, the quality of our air, the access to clean water, all provide the agency for us to live. While the world may seem to be chaotic, it also shares its wisdom if we only stop to look, listen, embrace, and learn. We can all be explorers looking into the interconnectivity of regeneration. The Earth is calling to every one of us to contribute new and innovative ways to steward our wetlands, grasslands, forests, coastlines, and all of the species that co-occupy our ocean and our land. What can you contribute?